10 bài toán Bồi dưỡng HSG Lớp 5 có lời giải
Gửi tới các em học sinh 10 bài toán Bồi dưỡng HSG Lớp 5 có lời giải. Những bài tập này rất có ích cho các bạn ôn thi học sinh giỏi.
Dưới đây là các bài tập.
Bài 1: Cho hai hình vuông ABCD và MNPQ như trong hình vẽ. Biết BD = 12 cm. Hãy tính diện tích phần gạch chéo.
Bài giải:
Diện tích tam giác ABD là : (12 x (12 : 2))/2 = 36 (cm2)
Diện tích hình vuông ABCD là : 36 x 2 = 72 (cm2)
Diện tích hình vuông AEOK là:
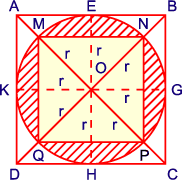
72 : 4 = 18 (cm2)
Do đó : OE x OK = 18 (cm2) r x r = 18 (cm2)
Diện tích hình tròn tâm O là :
18 x 3,14 = 56,92 (cm2)
Diện tích tam giác MON = r x r : 2 = 18 : 2 = 9 (cm2)
Diện tích hình vuông MNPQ là : 9 x 4 = 36 (cm2)
Vậy diện tích phần gạch chéo là :
56,52 – 36 = 20,52 (cm2)
Bài 2: Bạn Toàn nhân một số với 2002 nhưng “đãng trí” quên viết 2 chữ số 0 của số 2002 nên kết quả “bị” giảm đi 3965940 đơn vị. Toàn đã định nhân số nào với 2002 ?
Bài giải: Vì “đãng trí” nên bạn Toàn đã nhân nhầm số đó với 22.
Thừa số thứ hai bị giảm đi số đơn vị là : 2002 – 22 = 1980 (đơn vị).
Do đó kết quả bị giảm đi 1980 lần thừa số thứ nhất, và bằng 3965940 đơn vị. Vậy thừa số thứ nhất là : 3965940 : 1980 = 2003.
Bài 3: Người ta cộng 5 số và chia cho 5 thì được 138. Nếu xếp các số theo thứ tự lớn dần thì cộng 3 số đầu tiên và chia cho 3 sẽ được 127, cộng 3 số cuối và chia cho 3 sẽ được 148. Bạn có biết số đứng giữa theo thứ tự trên là số nào không ?
Bài giải: 138 là trung bình cộng của 5 số, nên tổng 5 số là : 138 x 5 = 690.
Tổng của ba số đầu tiên là : 127 x 3 = 381.
Tổng của ba số cuối cùng là : 148 x 3 = 444.
Tổng của hai số đầu tiên là : 690 – 444 = 246.
Số ở giữa là số đứng thứ ba, nên số ở giữa là : 381 – 246 = 135.
Bài 4: Cho bảng ô vuông gồm 10 dòng và 10 cột. Hai bạn Tín và Nhi tô màu các ô, mỗi ô một màu trong 3 màu : xanh, đỏ, tím. Bạn Tín bảo : “Lần nào tô xong hết các ô cũng có 2 dòng mà trên 2 dòng đó có một màu tô số ô dòng này bằng tô số ô dòng kia”. Bạn Nhi bảo : “Tớ phát hiện ra bao giờ cũng có 2 cột được tô như thế”. Nào, bạn hãy cho biết ai đúng, ai sai ?
Bài giải: Giả sử số ô tô màu đỏ ở tất cả các dòng đều khác nhau mà mỗi dòng có 10 ô nên số ô được tô màu đỏ ít nhất là : 0 + 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = 45 (ô).
Lí luận tương tự với màu xanh, màu tím ta cũng có kết quả như vậy. Do đó bảng sẽ có ít nhất 45 + 45 + 45 = 135 (ô). Điều này mâu thuẫn với bảng chỉ có 100 ô.
Chứng tỏ ít nhất phải có 2 dòng mà số ô tô bởi cùng một màu là như nhau. Đối với các cột, ta cũng lập luận tương tự như trên. Do đó cả hai bạn đều nói đúng.
Bài 5: Tìm 4 số tự nhiên có tổng bằng 2003. Biết rằng nếu xóa bỏ chữ số hàng đơn vị của số thứ nhất ta được số thứ hai. Nếu xóa bỏ chữ số hàng đơn vị của số thứ hai ta được số thứ ba. Nếu xóa bỏ chữ số hàng đơn vị của số thứ ba ta được số thứ tư.
Bài giải: Số thứ nhất không thể nhiều hơn 4 chữ số vì tổng 4 số bằng 2003. Nếu số thứ nhất có ít hơn 4 chữ số thì sẽ không tồn tại số thứ tư. Vậy số thứ nhất phải có 4 chữ số. Gọi số thứ nhất là abcd (a > 0, a, b, c, d < 10). Số thứ hai, số thứ ba, số thứ tư lần lượt sẽ là : abc ; ab ; a. Theo bài ra ta có phép tính :
abcd + abc + ab + a = 2003.
Theo phân tích cấu tạo số ta có : aaaa + bbb + cc + d = 2003 (*) Từ phép tính (*) ta có a < 2, nên a = 1. Thay a = 1 vào (*) ta được : 1111 + bbb + cc + d = 2003. bbb + cc + d = 2003 – 1111 bbb + cc + d = 892 (**)
b > 7 vì nếu b nhỏ hơn hoặc bằng 7 thì bbb + cc + d nhỏ hơn 892 ; b < 9 vì nếu b = 9 thì bbb = 999 > 892. Suy ra b chỉ có thể bằng 8. Thay b = 8 vào (**) ta được :
888 + cc + d = 892 cc + d = 892 – 888 cc + d = 4 Từ đây suy ra c chỉ có thể bằng 0 và d = 4.
Vậy số thứ nhất là 1804, số thứ hai là 180, số thứ ba là 18 và số thứ tư là 1. Thử lại : 1804 + 180 + 18 + 1 = 2003 (đúng)
Bài 6: Một người mang ra chợ 5 giỏ táo gồm hai loại. Số táo trong mỗi giỏ lần lượt là : 20 ; 25 ; 30 ; 35 và 40. Mỗi giỏ chỉ đựng một loại táo. Sau khi bán hết một giỏ táo nào đó, người ấy thấy rằng : Số táo loại 2 còn lại đúng bằng nửa số táo loại 1. Hỏi số táo loại 2 còn lại là bao nhiêu ?
Bài giải: Số táo người đó mang ra chợ là :
20 + 25 + 30 + 35 + 40 = 150 (quả)
Vì số táo loại 2 còn lại đúng bằng nửa số táo loại 1 nên sau khi bán, số táo còn lại phải chia hết cho 3.
Vì tổng số táo mang ra chợ là 150 quả chia hết cho 3 nên số táo đã bán phải chia hết cho 3. Trong các số 20, 25, 30, 35, 40 chỉ có 30 chia hết cho 3. Do vậy người ấy đã bán giỏ táo đựng 30 quả. Tổng số táo còn lại là : 150 – 30 = 120 (quả)
Ta có sơ đồ biểu diễn số táo của loại 1 và loại 2 còn lại:
![]()
Số táo loại 2 còn lại là :
120 : (2 + 1) = 40 (quả)
Vậy người ấy còn lại giỏ đựng 40 quả chính là số táo loại 2 còn lại. Đáp số : 40 quả
Bài 7: Không được thay đổi vị trí của các chữ số đã viết trên bảng : 8 7 6 5 4 3 2 1 mà chỉ được viết thêm các dấu cộng (+), bạn có thể cho được kết quả của dãy phép tính là 90 được không ?
Bài giải : Có hai cách điền :
8 + 7 + 65 + 4 + 3 + 2 + 1 = 90 8 + 7 + 6 + 5 + 43 + 21 = 90
Để tìm được hai cách điền này ta có thể có nhận xét sau :
Tổng 8 + 7 + 6 + 5 + 4 + 3 + 2 + 1 = 36 ; 90 – 36 = 54.
Như vậy muốn có tổng 90 thì trong các số hạng phải có một hoặc hai số là số có hai chữ số. Nếu số có hai chữ số đó là 87 hoặc 76 mà 87 > 54, 76 > 54 nên không thể được. Nếu số có hai chữ số là 65 ; 65 + 36 – 6 – 5 = 90, ta có thể điền :
8 + 7 + 65 + 4 + 3 + 2 + 1 – 90.
Nếu số có hai chữ số là 54 thì cũng không thể có tổng là 90 được vì 54 + 36 – 5 – 4 < 90. Nếu số có hai chữ số là 43 ; 43 < 54 nên cũng không thể được. Nếu trong tổng có 2 số có hai chữ số là 43 và 21 thì ta có 43 + 21 – (4 + 3 + 2 + 1) = 54. Như vậy ta có thể điền: 8 + 7 + 6 + 5 + 43 + 21 = 90.
Bài 8: Cho phân số M = (1 + 2 +… + 9)/(11 + 12 +… +19).
Hãy bớt một số hạng ở tử số và một số hạng ở mẫu số sao cho giá trị phân số không thay đổi.
Tóm tắt bài giải :
M = (1 + 2 +… + 9)/(11 + 12 +… +19) = 45/135 = 1/3.
Theo tính chất của hai tỉ số bằng nhau thì 45/135 = (45 – k)/(135 – kx3)(k là số tự nhiên nhỏ hơn 45). Do đó ở tử số của M bớt đi 4 ; 5 ; 6 thì tương ứng ở mẫu số phải bớt đi 12 ; 15 ; 18.
Bài 9:
Chỉ có một chiếc ca
Đựng đầy vừa một lít
Bạn hãy mau cho biết Đong nửa lít thế nào ?
Bài giải :
Ai khéo tay tinh mắt
Nghiêng ca như hình trên Sẽ đạt yêu cầu liền Trong ca : đúng nửa lít !
Bài 10: Điền số thích hợp theo mẫu :
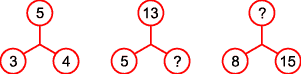
Bài giải : Bài này có hai cách điền:
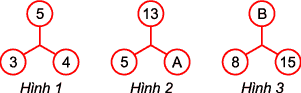
Cách 1: Theo hình 1, ta có 4 là trung bình cộng của 3 và 5 (vì (3 + 5) : 2 = 4).
Khi đó ở hình 2, gọi A là số cần điền, ta có A là trung bình cộng của 5 và 13.
Do đó A = (5 + 13) : 2 = 9.
ở hình 3, gọi B là số cần điền, ta có 15 là trung bình cộng của 8 và B. Do đó 8 + B = 15 x 2. Từ đó tìm được B = 22.
Cách 2: Theo hình 1, ta có 3 x 3 + 4 x 4 = 5 x 5.
Khi đó ở hình 2 ta có : 5 x 5 + A x A = 13 x 13.
suy ra A x A = 144. Vậy A = 12 (vì 12 x 12 = 144).
ở hình 3 ta có : 8 x 8 + 15 x 15 = B x B. suy ra B x B = 289. Vậy B = 17 (vì 17 x 17 = 289).
Toán lớp 5 - Tags: toán hsg