Bài tập tổng và hiệu của hai vectơ sách giáo khoa hình học 10
Timgiasuhanoi.com giải 1 số bài tập tổng và hiệu của hai vectơ trong sách giáo khoa hình học 10 cơ bản gồm: bài 3, bài 4 trang 7, bài 3 trang 12.
Sau khi đã học bài Tổng và hiệu của hai vectơ các em hãy đi vào giải các bài tập dưới đây.
Bài 3: (trang 7 SGK cơ bản)
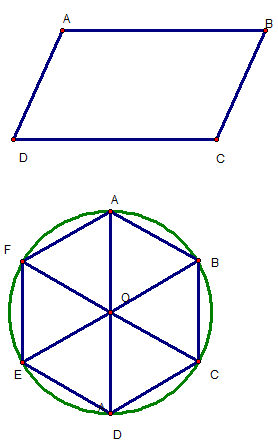
Cho tứ giác ABCD, Chứng minh rằng tứ giác ABCD là hình bình hành khi và chỉ khi .
Giải:
 Ta có, ABCD là hình bình hành:
Ta có, ABCD là hình bình hành:
=>AB // DC và AB = DC
hay cùng hướng và
=>
Ta lại có, :
=> cùng hướng và
hay AB // DC và AB = DC
=>ABCD là hình bình hành
Bài 4: (trang 7 SGK cơ bản)
Cho hình lục giác đều ABCDEF có tâm O.
- Tìm Véctơ khác
và cùng phương
.
- Tìm Véctơ bằng
.
Giải:
1. Các Véctơ khác và cùng phương
:
;
;
;
;
;
;
.
Véctơ bằng :
;
;
.
Bài 3: (trang 12 SGK cơ bản)
Chứng minh rằng đối mọi tứ giác ABCD bất kỳ, ta luôn có :
Giải:
1. Ta Áp dụng quy tắc 3 điểm cho phép cộng vectơ:
TA CÓ :
2.Ta Áp dụng quy tắc 3 điểm cho phép trừ vectơ:
=>
Bài 5: (trang 12 SGK cơ bản)
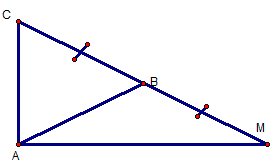 Cho tam giác đều ABC cạnh a. tính độ dài các vectơ :
Cho tam giác đều ABC cạnh a. tính độ dài các vectơ :
Giải:
Ta Áp dụng quy tắc 3 điểm cho phép cộng vectơ :
=>
Vẽ vectơ đối của : là vectơ
Ta được :
=>
Mặt khác : AB = BC = BM
=> tam giác AMC vuông tại A.
=> AM = a
Vậy :
==========================================
Bài tập tương tự:
Bài 1: Chứng minh rằng đối mọi tứ giác ABCD bất kỳ, ta luôn có :
Bài 2: Hình vuông ABCD cạnh a. Tính độ dài các vectơ :