Đề thi thử vào 10 môn Toán THPT chuyên Bắc Ninh 2020 có đáp án
Đề thi thử vào lớp 10 môn Toán dành cho học sinh thi vào trường THPT chuyên Bắc Ninh năm học 2020-2021. Có lời giải chi tiết để học sinh so sánh bài thi của mình.
Câu I. ( 1, 5 điểm )
Cho phương trình $\displaystyle {{x}^{2}}+2mx-2m-6=0$ (1) , với ẩn $\displaystyle x$, tham số m .
1) Giải phương trình (1) khi m = 1
2) Xác định giá trị của m để phương trình (1) có hai nghiệm $\displaystyle {{x}_{1}},{{x}_{2}}$ sao cho $\displaystyle {{x}_{1}}^{2},{{x}_{2}}^{2}$ nhỏ nhất.
Câu II. ( 1,5 điểm )
Trong cùng một hệ toạ độ , gọi (P ) là đồ thị của hàm số $\displaystyle y={{x}^{2}}$ và (d) là đồ thị của hàm số $\displaystyle y\text{ }=\text{ }-x\text{ }+\text{ }2$
1) Vẽ các đồ thị (P) và (d) . Từ đó , xác định toạ độ giao điểm của (P) và (d) bằng đồ thị .
2) Tìm a và b để đồ thị ∆ của hàm số $\displaystyle y\text{ }=\text{ }ax\text{ }+\text{ }b$ song song với (d) và cắt (P) tại điểm có hoành độ bằng -1
Câu III .( 2,0 điểm )
1) Một người đi xe đạp từ địa điểm A đến địa điểm B , quãng đường AB dài 24km . Khi đi từ B trở về A người đó tăng vận tốc thêm 4km so với lúc đi , vì vậy thời gian về ít hơn thời gian đi 30 phút . Tính vận tốc của xe đạp khi đi từ A đến B .
2 ) Giải phương trình $\displaystyle \sqrt{x}+\sqrt{{1-x}}+\sqrt{{x(1-x)}}=1$
Câu IV . ( 3,0 điểm )
Cho tam giác ABC có ba góc nhọn và ba đường cao AA’ , BB’ ,CC’ cắt nhau tại H .Vẽ hình bình hành BHCD . Đường thẳng qua D và song song với BC cắt đường thẳng AH tại M .
1) Chứng minh rằng năm điểm A, B ,C , D , M cùng thuộc một đường tròn.
2) Gọi O là tâm đường tròn ngoại tiếp tam giác ABC .Chứng minh rằng BM = CD và $\displaystyle \widehat{{BAM}}=\widehat{{OAC}}$ .
3) Gọi K là trung điểm của BC , đường thẳng AK cắt OH tại G . Chứng minh rằng G là trọng tâm của tam giác ABC.
Câu V .( 2, 0 điểm )
1) Tìm giá trị nhỏ nhất của biểu thức $\displaystyle P={{a}^{2}}+ab+{{b}^{2}}-3a-3b+2020$
2) Có 6 thành phố trong đó cứ 3 thành phố bất kỳ thì có ít nhất 2 thành phố liên lạc được với nhau. Chứng minh rằng trong 6 thành phố nói trên tồn tại 3 thành phố liên lạc được với nhau.
Đáp án Đề thi thử vào 10 môn Toán trường THPT chuyên Bắc Ninh 2020



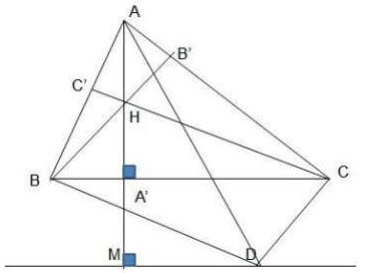
1) Chứng minh các tứ giác ABMD , AMDC nội tiếp
Do BHCD là hình bình hành nên:
Ta có: BD//CC’ ⇒ BD ⊥ AB ⇒ ABD = 90⁰
Có: AA’ ⊥ BC nên: MD ⊥ AA’ ⇒ AMD = 90⁰
⇒ ABD + AMD = 180⁰
⇒ tứ giác ABMD nội tiếp đường tròn đường kính AD.
Chứng minh tương tự ta có tứ giác AMDC nội tiếp đường tròn đường kính AD.
⇒ A, B ,C,D , M nằm trên cùng một đường tròn
2) Xét (O) có dây MD//BC ⇒ sđ cung MB = sđ cung CD ⇒ dây MB = dây CD hay BM = CD
+ Theo phần 1) và BC//MD ⇒ góc BAM = góc OAC
3) Chứng minh OK là đường trung bình của tam giác AHD ⇒ OK//AH và $\displaystyle OK=\frac{1}{2}AH$ hay $\displaystyle \frac{{OK}}{{AH}}=\frac{1}{2}$
+ Chứng minh tam giác OGK đồng dạng với tam giác HGA ⇒ $\frac{O K}{A H}=\frac{1}{2}=\frac{G K}{A G}$
⇒ $\displaystyle AG=2GK$
Câu V.( 2, 0 điểm )
1)
Ta có
$\displaystyle 4P={{a}^{2}}-2ab+{{b}^{2}}+3\left( {{{a}^{2}}+{{b}^{2}}+4+2ab-4a-4b} \right)+4.2020-12$
$\displaystyle \begin{array}{l}+4.2020-12\\=(a-b)2+3(a+b-2)2+8068\ge 8068\end{array}$
$\displaystyle \Rightarrow P\ge 2017$
Dấu “=” xảy ra ⇔$\displaystyle \left\{ {\begin{array}{*{20}{l}} {a=b} \\ {a+b-2=0} \end{array}} \right.$
⇒ a = b = 1
Vậy giá trị nhỏ nhất của P là 2017 khi và chỉ khi a = b = 1.
2) Gọi 6 thành phố đã cho là A,B,C,D,E,F
+ Xét thành phố A .theo nguyên l í Dirichlet ,trong 5 thành phố còn lại thì có ít nhất 3 thành phố liên lạc được với A hoặc có ít nhất 3 thành phố không liên lạc được với A ( vì nếu số thành phố liên lạc được với A cũng không vượt quá 2 và số thành phố không liên lạc được với A cũng không vượt quá 2 thì ngoài A , số thành phố còn lại cũng không vượt quá 4 ) . Do đó chỉ xảy ra các khả năng sau :
* Khả năng 1 : số thành phố liên lạc được với A không ít hơn 3 , giả sử B,C,D liên lạc được với A . Theo đề bài trong 3 thành phố B,C,D có 2 thành phố liên lạc được với nhau . Khi đó 2 thành phố này cùng với A tạo thành 3 thành phố đôi một liên lạc được với nhau .
* Khả năng 2 : số thành phố không liên lạc được với A , không ít hơn ,giả sử 3 thành phố không liên lạc được với A là D,E,F. Khi đó trong bộ 3 thành phố ( A,D,E) thì D và E liên lạc được với nhau ( v ì D,E không liên lạc được với A)
Tương tự trong bộ 3 ( A,E,F) v à ( A,F,D) th ì E,F liên lạc được với nhau , F và D liên lạc được với nhau và như vậy D,E,F l à 3 thành phố đôi một liên lạc được với nhau .
Vậy ta có ĐPCM.
Đề thi Toán vào lớp 10 - Tags: đề thi thử, đề thi thử vào 10, THPT chuyên Bắc Ninh43 Đề thi thử vào 10 môn Toán năm học 2020 – 2021
Đề thi môn Toán vào lớp 10 THPT chuyên Thái Bình năm 2019-2020
Đề thi thử vào 10 môn Toán THCS Cao Bá Quát lần 2 năm học 2018-2019
Đề thi thử vào 10 môn Toán Hà Nội Amsterdam đợt 1 ngày 24/3/2019
Tuyển tập các bài Hình học trong đề thi vào lớp 10 Hà Nội từ 2006 tới nay
Đề thi thử vào lớp 10 môn Toán THCS Ngôi Sao Hà Nội 2018 có đáp án
Đề thi Toán vào lớp 10 Thái Nguyên năm học 2018-2019 có đáp án