Đề thi tuyển sinh vào 10 môn Toán tỉnh Bắc Giang 2017 – 2018 có đáp án
Đề thi tuyển sinh môn Toán vào lớp 10 trung học phổ thông. Sở giáo dục và đào tạo Bắc Giang. Ngày thi 06/06/2017. Có đáp án.
Thời gian làm bài 120 phút, không kể thời gian giao đề.
Đề thi:
Câu I (2,0 điểm).
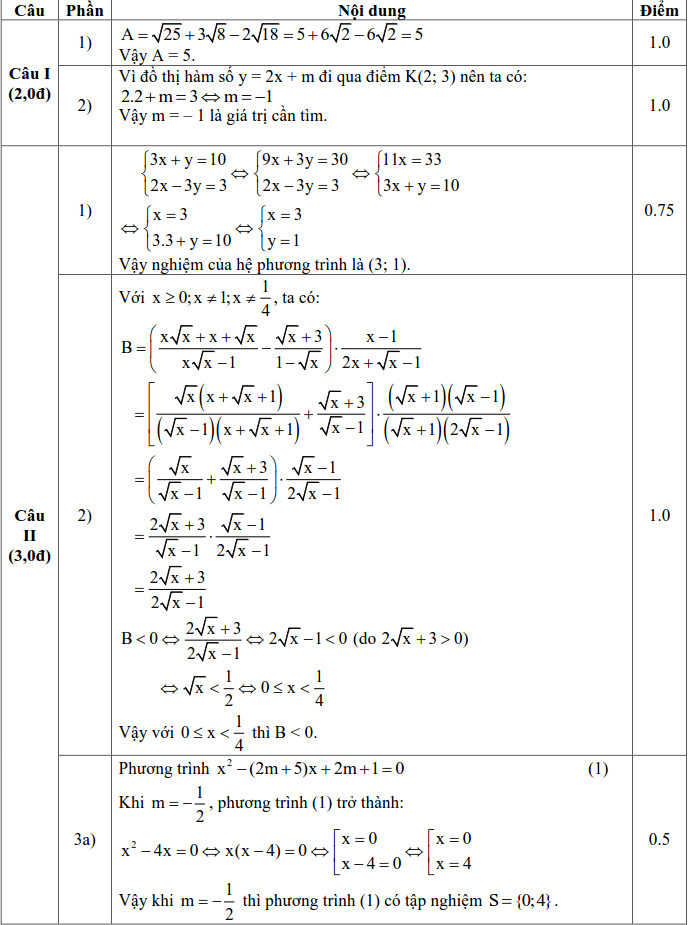
- Tính giá trị của biểu thức $ A=\sqrt{25}+3\sqrt{8}-2\sqrt{18}$.
- Tìm $ m$ để đồ thị hàm số $ y=2x+m$ đi qua điểm $ K(2;3)$.
Câu II (3,0 điểm).
- Giải hệ phương trình $ \left\{ \begin{array}{l}3x+y=10\\2x-3y=3\end{array} \right.$.
- Cho biểu thức $ B=\left( \frac{x\sqrt{x}+x+\sqrt{x}}{x\sqrt{x}-1}-\frac{\sqrt{x}+3}{1-\sqrt{x}} \right).\frac{x-1}{2x+\sqrt{x}-1}$ (với $ x\ge 0;\,\,x\ne 1$ và $ x\ne \frac{1}{4}$).
Tìm tất cả các giá trị của $ x$ để $ B<0$.
- Cho phương trình $ {{x}^{2}}-(2m+5)x+2m+1=0$ (1), với $ x$ là ẩn, $ m$ là tham số.
- Giải phương trình (1) khi $ m=-\frac{1}{2}$.
- Tìm các giá trị của để phương trình (1) có hai nghiệm dương phân biệt $ {{x}_{1}},\,\,{{x}_{2}}$ sao cho biểu thức $ P=\left| \sqrt{{{x}_{1}}}-\sqrt{{{x}_{2}}} \right|$ đạt giá trị nhỏ nhất.
Câu III (1,5 điểm).
Để chuẩn bị cho năm học mới, học sinh hai lớp 9A và 9B ủng hộ thư viện 738 quyển sách gồm hai loại sách giáo khoa và sách tham khảo. Trong đó mỗi học sinh lớp 9A ủng hộ 6 quyển sách giáo khoa và 3 quyển sách tham khảo; mỗi học sinh lớp 9B ủng hộ 5 quyển sách giáo khoa và 4 quyển sách tham khảo. Biết số sách giáo khoa ủng hộ nhiều hơn số sách tham khảo là 166 quyển. Tính số học sinh của mỗi lớp.
Câu IV (3,0 điểm).
Cho tam giác $ ABC$ có ba góc nhọn, nội tiếp đường tròn $ \left( C \right)$ tâm $ O$ bán kính $ R$. Hai đường cao $ AE$ và $ BK$ của tam giác $ ABC$ cắt nhau tại $ H$ (với $ E$ thuộc $ BC$, $ K$ thuộc $ AC$).
- Chứng minh tứ giác $ ABEK$ nội tiếp được trong một đường tròn.
- Chứng minh $ CE.CB=CK.CA$.
- Chứng minh $ \widehat{OCA}=\widehat{BAE}$.
- Cho $ B,\,\,C$ cố định và $ A$ di động trên $ \left( C \right)$ nhưng vẫn thoả mãn điều kiện tam giác $ ABC$ nhọn; khi đó $ H$ thuộc một đường tròn $ \left( T \right)$ cố định. Xác định tâm $ I$ và tính bán kính $ r$ của đường tròn $ \left( T \right),$ biết $ R=3\,cm$.
Câu V (0,5 điểm).
Cho hai số thực dương $ a,\,\,b$ thoả mãn $ 2a+3b\le 4$. Tìm giá trị nhỏ nhất của biểu thức $ Q=\frac{2002}{a}+\frac{2017}{b}+2996a-5501b$.
Hướng dẫn giải và biểu điểm dự kiến:



Đề thi vào 10 môn Toán – Quảng Ninh năm 2012 – 2013 có đáp án
Đề thi vào 10 môn Toán – Bắc Giang năm 2012 – 2013 có đáp án
Đề thi vào 10 môn Toán – Bắc Ninh năm 2012 – 2013 có đáp án
Đề thi vào 10 môn Toán – Bình Định năm 2012 – 2013 có đáp án
Đề thi vào 10 môn Toán – Bình Dương năm 2012 – 2013 có đáp án
Đề thi vào 10 môn Toán – Hà Tĩnh năm 2012 – 2013 có đáp án
Đề thi vào 10 môn Toán – Hà Nội năm 2012 – 2013 có đáp án