Một số sai lầm khi giải phương trình lượng giác

Gia sư Hà Nội đưa ra một số sai lầm của học sinh khi giải phương trình lượng giác qua các ví dụ minh họa và phương hướng khắc phục.

Chúng tôi chỉ nêu ra một số sai lầm cơ bản sau:

Học sinh đôi khi còn nhầm lẫn giữa giá trị lượng giác của một cung đặc biệt và một cung đặc biệt

Ví dụ: Giải phương trình sau: $ \displaystyle \sin x=\frac{1}{2}$

* Sai lầm thường gặp:

$ \displaystyle \sin x=\frac{1}{2}\Leftrightarrow \sin x=\frac{\pi }{6}$

$ \displaystyle \Leftrightarrow \left[ \begin{array}{l}x=\frac{\pi }{6}+k2\pi \\x=\frac{5\pi }{6}+k2\pi \end{array} \right.$ (k ∈ Z)

* Hướng khắc phục

Học sinh cần phân biệt rõ một cung đặc biệt và giá trị sin của một cung đặc biệt $ \displaystyle \frac{1}{2}\ne \frac{\pi }{6}$

* Lời giải đúng:

$ \displaystyle \sin x=\frac{1}{2}\Leftrightarrow \sin x=\sin \frac{\pi }{6}$

$ \displaystyle \Leftrightarrow \left[ \begin{array}{l}x=\frac{\pi }{6}+k2\pi \\x=\frac{5\pi }{6}+k2\pi \end{array} \right.$ (k ∈ Z)

Vậy nghiệm của phương trình là: $ \displaystyle x=\frac{\pi }{6}+k2\pi $ và $ \displaystyle x=\frac{5\pi }{6}+k2\pi $ (k ∈ Z).

Ví dụ: Giải phương trình sau:

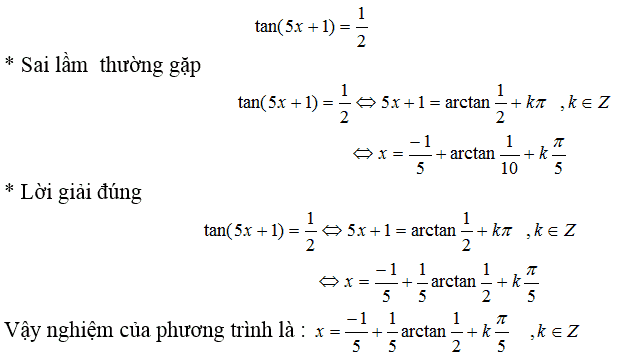
Một số sai lầm khi giải phương trình lượng giác

Học sinh nhiều khi trong một công thức nghiệm lại có tới 2 đơn vị đo độ và rađian

Ví dụ: Giải phương trình sau: $ \displaystyle \sin (2x+15{}^\circ )=\frac{\sqrt{3}}{2}$

* Sai lầm thường gặp:

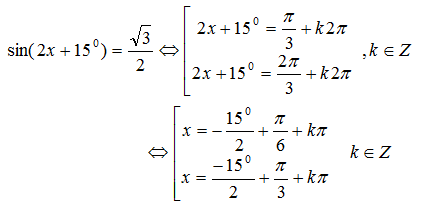
Một số sai lầm khi giải phương trình lượng giác-1

* Lời giải đúng:

Vậy nghiệm của phương trình là:

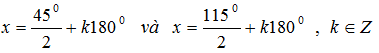
Nếu còn thiếu sai lầm hoặc lỗi nào hay gặp phải khi giải phương trình lượng giác thì các bạn hãy trả lời ngay bên dưới để Gia sư Hà Nội bổ sung nhé.